JS 기본 자료구조 - 링크드 리스트, 해시태이블, 그래프, 이진탐색트리

매우 주관적인 포스트로서 사실과 다를수도 있습니다. 개인적인 정리 차원입니다.

​

링크드 리스트

링크드 리스트는 내가 기억하기로는 메모리 공간 사용을 효율적으로 하기위해서 사용한다고 배웠던 기억이 있다.

이게 C++ 에서 그런지 어딘지는 확실하지 않다. (사실 자바스크립트 배열이 링크드 리스트를 사용한다.) ​

우선 대략적인 구조는 다음과 같다. ​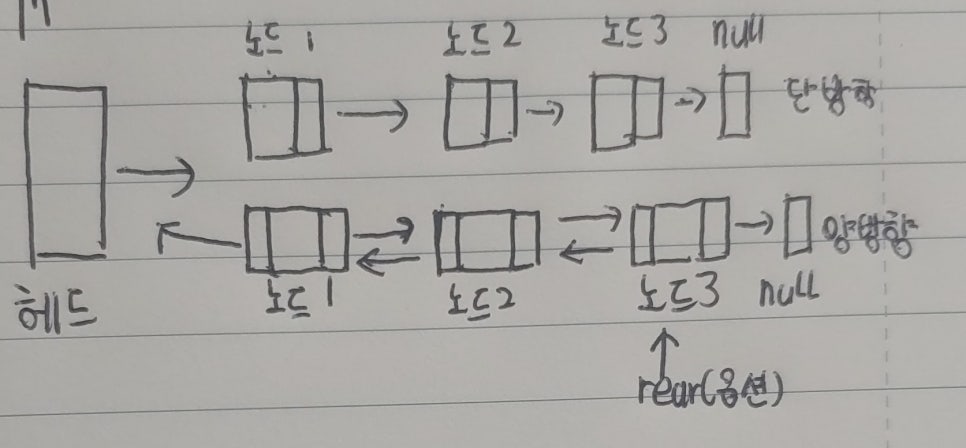 내 머리속에 대략적인 구상

구성하는 요소들은 다음과 같다.

1. 헤드(head) 리스트가 처음에 실행될 때 부터 존재한다. 기본적으로 처음에 생성되는 노드는 헤드와 연결해야 한다. 즉 헤드는 첫 번째 노드를 가르키게 된다. 일종에 포인터 이며, 생성후 값은 별로 바꾸지 않는다.

2. 노드(node) 어떤 벨류들을 가지고 있으며, 이후에 생성되는 노드와 연결된다. 또한 이전의 노드와 연결시켜 양방향 리스트로 제작할수 있다.

노드들 양쪽 혹은 한쪽에 작은 직사각형들은 다음/이전 노드의 메모리 위치를 가리키고 있는 포인터들.

​

1. 리어(rear) 마지막 노드를 가리키고 있다. 마지막 요소를 리턴해야 하는 경우에 요긴하게 쓰일 수 있다.(처음부터 끝가지 탐색하여 끝 노드의 값을

찾아내는것은 매우 오래걸릴수도 있지 않을까 해서 추가, 선택사항)

​

저 헤드와 노드들은 화살표로 연결 시켜 놓았다. 앞서 말했듯이 한쪽 혹은 양쪽의 노드들의 메모리 주소를 담고 있다.

이런 구성때문에 메모리 활용에서 속도는 늦을지언정, 공간활용도가 아주 좋다. 적절한 빈공간만 있으면 정보를 담고, 다음/이전 노드 메모리 주소만 작성하면 연결이 된다.

​ 노드 추가와 마찬가지로 노드 삭제도 간편하다. 이전/이후 노드끼리 메모리 위치만 교환하고, 해당 노드를 지워 버리면 된다.

다만 노드 탐색이 매우 힘들수 있다. 처음부터 탐색하여 원하는 값을 찾아야 하는 경우에는 모든 노드를 다 찾아봐야 원하는 값을 찾을 수 있을것이다. ​

그렇기 때문에 일직선이 아닌 다른 구조로 정리 해 놓고 사용하기도 한다.

​

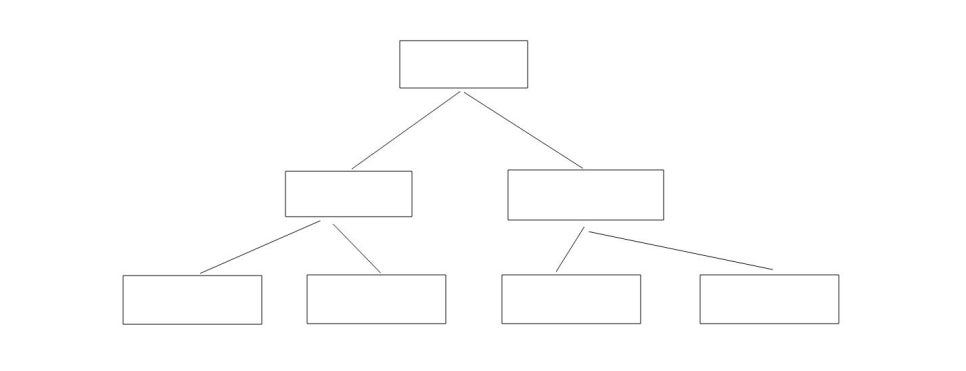
트리 구조의 링크드 리스트

트리구조는 간략히 설명하자면, 어떤 노드는 아래에 달린 노드들 전부 보다 크거나 한쪽보다 작거나 커야 한다.

이를 어기는 노드는 노드의 값들을 서로 바꿔야 한다.

아래에 달린 노드들의 분류는 오름차순 혹은 내림차순으로 정렬 할 수도 있으며, 이를 지키지 않는 노드들간에도 값을 교환 해야 한다.

위와 같은 경우에는 이진 탐색 트리가 될수 있다. ​

적용하는 룰은 오름차순, 내림차순등등을 필요에 따라 적용한다. 아래에 달린 노드의 수도 필요에 따라 결정한다. 위의 경우는 이진 트리가 될것이다. 자세한건 아래로 가서 정리해 본다. ​

다시 돌아와서 일직선 리스트에서 만약 끝의 노드가 처음을 가리키게 하면 바로 원형 리스트가 된다. ​

만약 구현한다면 필요한 메소드들은

size, delete, add, find, modify, init 정도?

​### 메서드 size 함수는 총 리스트의 크기를 반환하게 될것이며,

find 함수는 리스트 어딘가에 존재하는 노드를 찾아서 리턴해야 하며

add 함수는 리스트 끝 혹은 어딘가에 노드를 추가해야 할것이며

delete 함수는 어딘가의 노드만 삭제해야 할것이다(헤드는 지워버리면 리스트 접속이 불가능 하다)

init 함수는 리스트 초기화를 해야 하며, 모든 노드 들을 지워버리고 NULL을 가리키고 있게 만든다. 사이즈도 초기화 한다.

head와 rear 포인터를 가지게 되며

size 라는 변수를 가지고 크기를 작성하게 될것이다.

또한 노드라는 어떤 객체를 필요로 하며, head와 rear는 이 객체의 일종이 되야 할것이다.

​

노드는 데이터를 저장할 변수와, 양방향/단방향 포인터를 가지게 될것이다.

노드는 next/before 함수를 이용하여 이전/이후 노드로 포인터를 이동 시킬수 있어야 한다.

노드는 자신의 변수를 반환하는 get 함수, 설정하는 set 함수가 필요할것 같다.

​

해시 테이블

해시 테이블은 배운지 가물가물하니 구글신을 영접해 찾아 보았다.

우선 기억속의 해시 테이블은

무한수를 테이블 속에 일부만 집어넣은것이며, 인풋을 받아 해시 테이블을 보고 특정한 다른것에 연결시켜서 뭐 보안쪽에서도 쓰이고

그런다고 배운것 같다. 그래 구글신이 키 - 매핑 테이블이라고 하니 이게 정확해 보인다.

​

해시 테이블은 효율적이고, 삽입과 삭제에 큰 시간을 필요하지 않으며, 적은 테이블로도 관리가 용이해 진다. 라고 한다.

그러고 보니 입력값 전부를 저장하는것 보다는 해싱을 한 결과물을 관리하는것이 좋아보인다. 그 거대한 데이터를 저장하는 것보다는 차라리 해싱을 하여 색인 작업을 하는것이 효율적인것이 맞는것 같다. 또한 그냥 색인들만 보면 되니 탐색, 삽입, 삭제도 그렇게 오래 걸리지 않는것이 맞는것 같다.

​

하지만

비교적 인풋을 받아 어떤 함수로 키와 벨류를 매핑 시키는 것은 비교적 좋아 보일수 있으나

해시테이블은 유한하다. 즉 언젠가는 키 매핑이 중복된다. 그러니까 a라는 사람이 입력한 값과 b라는 사람이 입력한 값이

같아질수 있다. 둘은 서로 다른 값을 인풋으로 집어 넣은 상태다. 고로 b라는 사람이 a인것처럼 접속할수 있다는 것이다.

이것을 해시 충돌이라고 배웠다.

​

몇년전에 해쉬를 가지고 개인 프로젝트로 해싱을 마구잡이로 하던 적이 있었다. 그때는 MD5라는 해싱 기법을 이용하고 있었는데,

언젠가 테스트를 하다보니 값이 이상해서 보니 서로 다른 인풋이 해시 충돌을 하고 있었다. 비교적 크지 않은 해시 테이블과 인풋량 이였는데도 충돌난것이 묘하게 신기했었다. 하지만 MD5 알고리즘은 이미 해시값으로 인풋값을 알아내는 공격이 성공한 알고리즘이기 때문에 비교적 최근에 나온 다른 알고리즘을 쓰는게 좋을것이다.

​

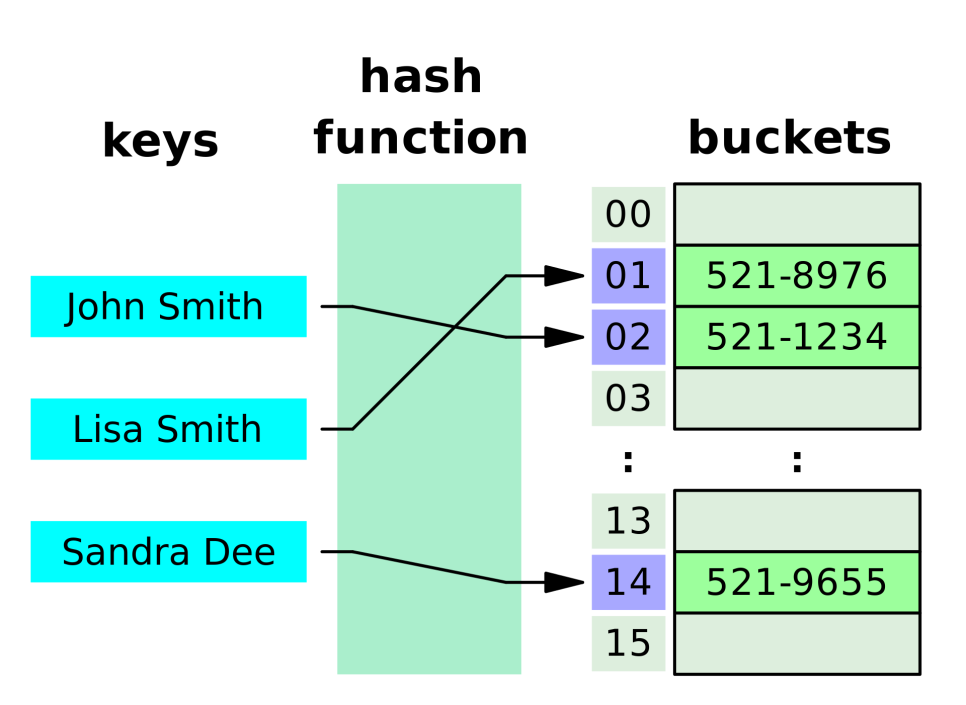​ 해시 테이블의 구조 - Wikipedia

위키 피디아에서 사진을 가져왔다. 보다 싶이 무한수를 입력하여 15개의 테이블에 매핑한다.

키를 해시하여 펑션 사용할 버켓을 정하게 된다.

​

그러므로 만약 구현 한다면

버켓을 초기화 하는 init, 해시 펑션, 해시 값을 보고 맞는 버켓을 리턴할 버켓 함수, 버켓 수정 함수 가 필요하지 않을까 싶다.

​

프로퍼티 들로는

해시 테이블, 버켓, 테이블 크기 정도?

​

그래프

그래프도 일종의 링크드 리스트로 구현 가능하다. 다만 연결할 링크가 한개일수도 2개 이상 일수도 있다.

그래프를 보니 어디서 봤던건가 했더니, 길 찾기 알고리즘에서 봤던 거다. (다익스트라… 메모….)

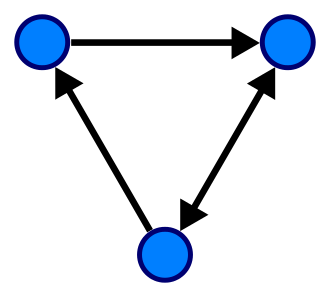​ 그래프의 일종 - Wikipedia

위에서 보이는것은 일부 노드가 단방향으로 연결되어 있다. 물론 양방향으로 연결할 수 도 있을 것이다.

물론 저기서 연결이 안되도 무관 하다. 저기서 만약 화살표에 관계의 강도를 표현할 수도 있다.

​

지금 느끼는 바로는 약간 관계망을 그리는것 같은 느낌이 강하다.

​

위키 피디아에 따르면, 리스트 자료구조 와 행렬 자료 구조를 사용하여 표현이 가능하다고 하다.

리스트는 노드 별로 연결된 노드들을 리스트로 가진다. 메모리 사용량은 낮으나 속도가 문제가 될수 있다.

행렬은 행렬로 연결을 표현한다. 메모리 사용량은 높으나 리스트 보다는 빠를것이다.

​

만약 노드들을 연결한 링크까지 고려 하고, 위키피디아 에서 추천하는 링크드 + 행렬 방식으로 구현한다손 치면

​

프로퍼티

헤드 노드, 행렬(아마도 배열) 이 필요할 것이고,가장긴 거리 와 가장 짦은 거리, 센트럴 포인트, 센트럴 포인트에서 가장 긴 거리, 노드를 거처서 다시 돌아올수있는 수, 가장 짦은 순환가능 거리, 가장 긴 순환 가능 거리를 변수로 가진다고 한다.(JAVA Point 참고)

​

메소드 들은

add, delete, find, edge(fix, add, delete를 옵션으로 설정),size, circle(순환 가능한 노드들의 수), find_central, maxDisFromCent, shortCircle, longCircle을 함수로 가지지 않을까 싶다.

​

노드들은

data 변수,data 리턴 함수, 연결 가능 노드 리스트(아마도 배열)와 엣지 크기, 다른 노드로 이동하는 goto()을 매서드와 프로퍼티로 가지지 않을까 싶다.

​

#나중을 위해 위키피디아의 그래프 프로퍼티 링크를 남긴다.

https://en.wikipedia.org/wiki/Graph_property#Properties

트리

트리는 위에서 연결 리스트에 대하여 작성할때 맛보기로 보여준 적이 있다.

​

이진 트리

이게 바로 트리 구조이다. 맨 위에 노드가 root라 부른다. 생긴게 뿌리 같아서 인가 아니면 나무잎이 퍼지는 모양새이라그런지 트리라는 이름과

루트라는 이름이 사용된다.

​

연결하는 방식은 단방향 으로서, 루트에서 아래쪽으로 연결 할 수는 있지만, 반대로 아래 노드에서 루트 노드 쪽으로 연결이 불가능하다.

앞서 말했듯이 한개의 노드에서 여러 노드를 연결 하되, 연결된 노드로 양방향 연결은 불가능 하다.

​

노드들은 루트 노드, 중간 노드, 리프 노드라 부르는데, 루트는 근원인 최 상위 노드 이고, 리프 노드는 최 말단으로서 연결할 노드가 없는 노드들 이다. 위 그림에는 리프 노드가 4개 있는 셈. 나머지들은 중간 노드라 부른다.

만약에 한쪽으로만 계속 노드들을 추가한다면 그건 단 방향 링크드 리스트가 된다.

​

​

트리중에서는 이진 트리를 설명하자면,

상위 노드(부모노드)는 아래 하위노드(자식노드)로 단 2개까지만 노드로 가진다.

​

이 이진트리가 여기 저기서 사용되는데, 그중에 오늘 정리할 이진 탐색 트리도 있다.

이진트리는 앞서 설명했듯이 트리구조로 정리해 나가는 것이다.

​

규칙은 다음과 같다. (Wikipedia)

1. 각 노드에 값이 있다. 값들은 전순서가 있다.

2. 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.

3. 노드의 오른쪽 서브트리에는 그 노드의 값과 같거나 큰 값들을 지닌 노드들로 이루어져 있다.

4. 좌우 하위 트리는 각각이 다시 이진 탐색 트리여야 한다.

​

이에 맞춰 위키 피디아의 예제를 설명해 보자면 ​ ​

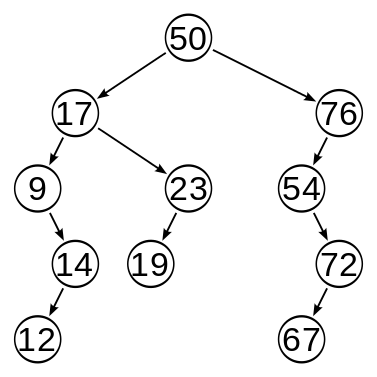
현재 상황은 리프로드에 12와 67, 72이 삽입된 상태이다. 룰을 만족하나, 이 트리를 더욱 정리 할 수 있다.

보변 이진 트리의 룰을 전부 만족하면서, 메모리에 접근하는 빈도가 더욱 낮아졌다. 즉 속도가 높아졌다.

이런 트리 구조를 이진 탐색 트리라 한다.

수정 방법은 아마 왼쪽 서브 트리의 가장 큰값과 비교하거나, 오른쪽 서브트리의 가장 작은 값과 비교하여 치환 하지 않을까?

그다음 트리를 룰에 따라 수정하면 될것이다.

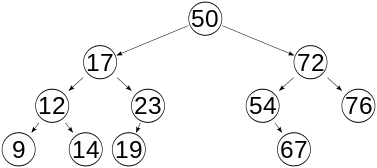​ 이 트리들은 프로퍼티로

depth, size, root 포인터를 반드시 가지고 있을 것이며

​

함수들은 add(item), delete(item), 사이즈와 뎊스를 리턴하는 함수, 이진트리라면 트리를 수정하는 fix()를 가지고 있을것이다.